The Hilger derivative on a time scale is defined by
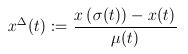 . .
For discrete time,
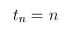
and
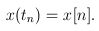
The Hilger derivative becomes the first order difference for discrete time.
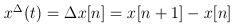 . .
For continuous time, the Hilger derivative is taken in the limit sense and is the conventional continuous time derivative.
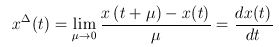 . .
Integration on a time scale can be viewed as an antiderivative. If we have the time scale derivative
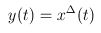 , ,
then the antiderivative is
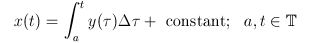 , ,
and the definite integral on a time scale follows as
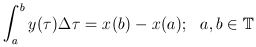 . .
|