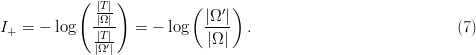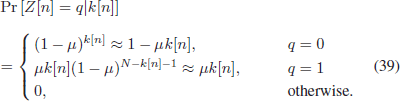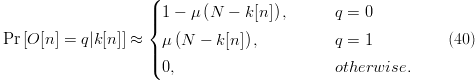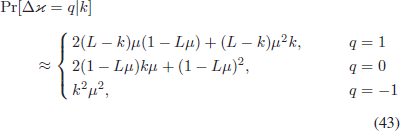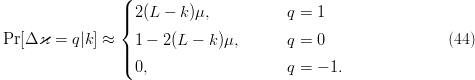SECTION I
INFORMATION AS A COST OF SEARCH
OVER 50 years ago, Leon Brillouin,
a pioneer in information theory, wrote “The [computing] machine does
not create any new information, but it performs a very valuable
transformation of known information” [5]. When
Brillouin's insight is applied to search algorithms that do not employ
specific information about the problem being addressed, one finds that
no search performs consistently better than any other. Accordingly, there is no “magic-bullet” search algorithm that successfully resolves all problems [10], [44].
In the last decade, Brillouin's insight has been analytically
formalized under various names and in various ways in regard to
computer-optimization search and machine-learning algorithms.
- Schaffer's Law of Conservation of Generalization Performance [39]
states “a learner … that achieves at least mildly better-than-chance
performance [without specific information about the problem in
question]… is like a perpetual motion machine.”
- The no free lunch theorem (NFLT) [46] likewise establishes the need for specific information about the search target to improve the chances of a successful search.
“[U]nless you can make prior assumptions about the … [problems] you are
working on, then no search strategy, no matter how sophisticated, can
be expected to perform better than any other” [23].
Search can be improved only by “incorporating problem-specific
knowledge into the behavior of the [optimization or search] algorithm” [46].
- English's Law of Conservation of Information (COI) [15]
notes “the futility of attempting to design a generally superior
optimizer” without problem-specific information about the search.
When applying Brillouin's insight to search algorithms (including
optimization, machine-learning procedures, and evolutionary computing),
we use the umbrella-phrase COI. COI establishes that one search
algorithm will work, on average, as well as any other when there is no
information about the target of the search or the search space. The
significance of COI has been debated since its popularization through
the NFLT. On the one hand, COI has a leveling effect, rendering the
average performance of all algorithms equivalent. On the other hand,
certain search techniques perform remarkably well, distinguishing
themselves from others. There is a tension here, but no contradiction. For instance, particle-swarm optimization [2], [14], [16], [22] and genetic algorithms [1], [16], [19], [36], [37], [38], [45], [49], [51] perform well on a wide spectrum of problems.
Yet, there is no discrepancy between the successful experience of
practitioners with such versatile search algorithms and the COI-imposed
inability of the search algorithms themselves to create novel
information [7], [13], [15].
Such information does not magically materialize but instead results
from the action of the programmer who prescribes how knowledge about the
problem gets folded into the search algorithm.
Practitioners in the earlier days of computing sometimes referred to themselves as “penalty function artists” [21],
a designation that reflects the need for the search practitioner to
inject knowledge about the sought-after solution into the search
procedure. Problem-specific information is almost always embedded in
search algorithms. Yet, because this information can be so familiar, we
can fail to notice its presence.
COI does not preclude better-than-average performance on a specific problem class [8], [18], [20], [31], [35], [43]. For instance, when choosing the best 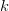 $k$ of
$k$ of 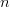 $n$ features for a classification problem, hill-climbing approaches are much less effective than branch-and-bound approaches [25].
Hill-climbing algorithms require a smooth fitness surface
uncharacteristic of the feature-selection problem. This simple insight
when smooth fitness functions are appropriate constitutes knowledge
about the search solution; moreover, utilizing this knowledge injects
information into the search. Likewise, the ability to eliminate large
regions of the search space in branch-and-bound algorithms supplies
problem-specific information. In these examples, the information source
is obvious. In other instances, it can be more subtle.
$n$ features for a classification problem, hill-climbing approaches are much less effective than branch-and-bound approaches [25].
Hill-climbing algorithms require a smooth fitness surface
uncharacteristic of the feature-selection problem. This simple insight
when smooth fitness functions are appropriate constitutes knowledge
about the search solution; moreover, utilizing this knowledge injects
information into the search. Likewise, the ability to eliminate large
regions of the search space in branch-and-bound algorithms supplies
problem-specific information. In these examples, the information source
is obvious. In other instances, it can be more subtle.
Accuracy of problem-specific information is a fundamental requirement
for increasing the probability of success in a search. Such information
cannot be offered blindly but must accurately reflect the location of
the target or the search-space structure. For example, to open a locked
safe with better-than-average performance, we must either do the
following.
- Know something about the combination, e.g., knowing all of the
numbers in the combination are odd is an example of target information.
- Know something about how the lock works, e.g., listening to the
lock's tumblers during access is an example of search-space structure
information.
In either case, the information must be accurate. If we are
incorrectly told, for example, that all of the digits to a lock's
combination are odd when in fact they are all even, and we therefore
only choose odd digits, then the probability of success nosedives. In
that case, we would have been better simply to perform a random search.
Recognition of the inability of search
algorithms in themselves to create information is “very useful,
particularly in light of some of the sometimes-outrageous claims that
had been made of specific optimization algorithms” [7].
Indeed, when the results of an algorithm for even a moderately sized
search problem are “too good to be true” or otherwise “overly
impressive,” we are faced with one of two inescapable alternatives.
- The search problem under consideration, as gauged by random
search, is not as difficult as it first appears. Just because a
convoluted algorithm resolves a problem does not mean that the problem
itself is difficult. Algorithms can be like Rube Goldberg devices that
resolve simple problems in complex ways. Thus, the search problem itself
can be relatively simple and, from a random-query perspective, have a
high probability of success.
- The other inescapable alternative, for difficult problems, is that
problem-specific information has been successfully incorporated into the
search.
As with many important insights, reflection reveals the obviousness
of COI and the need to incorporate problem-specific information in
search algorithms. Yet, despite the widespread dissemination of COI
among search practitioners, there is to date no general method to apply
COI to the analysis and design of search algorithms. We propose a method
that does so by measuring the contribution of problem-specific target
and search-space structure information to search problems.
SECTION II
MEASURING ACTIVE INFORMATION
If we have a combination lock with five thumb wheels, each numbered
from zero to nine, our chances of opening the lock in eight tries or
less is not dependent on the ordering of the combinations tried. Using
the results of the first two failed combinations, for example, [0, 1, 2,
3, 4] and [4, 3, 2, 1, 0], tells us nothing about what the third try
should be. After eight tries at the combination lock with no duplicate
combinations allowed, no matter how clever the method used, the chances
of choosing the single combination that opens the lock is 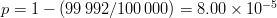 $p = 1 - (99\,992/100\,000) = 8.00 \times 10^{-5}$ corresponding to an endogenous information of
$p = 1 - (99\,992/100\,000) = 8.00 \times 10^{-5}$ corresponding to an endogenous information of 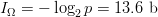 $I_{\Omega} = -\log_{2}p = 13.6\ \hbox{b}$.
The endogenous information provides a baseline difficulty for the
problem to be solved. In this example, the problem difficulty is about
the same as sequentially forecasting the results of 14 flips of a fair
coin.
$I_{\Omega} = -\log_{2}p = 13.6\ \hbox{b}$.
The endogenous information provides a baseline difficulty for the
problem to be solved. In this example, the problem difficulty is about
the same as sequentially forecasting the results of 14 flips of a fair
coin.
To increase the probability of finding the correct combination, more
information is required. Suppose, for example, we know that all of the
single digits in the combination that opens the lock are even. There are
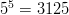 $5^{5} = 3125$ such combinations. Choosing the single successful combination in eight tries or less is
$5^{5} = 3125$ such combinations. Choosing the single successful combination in eight tries or less is 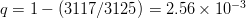 $q = 1 - (3117/3125) = 2.56 \times 10^{-3}$, or exogenous information
$q = 1 - (3117/3125) = 2.56 \times 10^{-3}$, or exogenous information 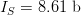 $I_{S} = 8.61\ \hbox{b}$. The difference,
$I_{S} = 8.61\ \hbox{b}$. The difference, 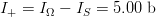 $I_{+} = I_{\Omega} - I_{S} = 5.00\ \hbox{b}$, is the active information and assesses numerically the problem-specific information incorporated into the search that all the digits are even.
$I_{+} = I_{\Omega} - I_{S} = 5.00\ \hbox{b}$, is the active information and assesses numerically the problem-specific information incorporated into the search that all the digits are even.
More formally, let a probability space 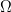 $\Omega$ be partitioned into a set of acceptable solutions
$\Omega$ be partitioned into a set of acceptable solutions 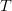 $T$ and a set of unacceptable solutions
$T$ and a set of unacceptable solutions 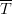 $\overline{T}$. The search problem is to find a point in
$\overline{T}$. The search problem is to find a point in 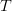 $T$ as expediently as possible. With no problem-specific information, the distribution of the space is assumed uniform. This assumption dates to the 18th century and Bernoulli's principle of insufficient reason [4], which states that “in the absence of any prior knowledge, we must assume that the events [in
$T$ as expediently as possible. With no problem-specific information, the distribution of the space is assumed uniform. This assumption dates to the 18th century and Bernoulli's principle of insufficient reason [4], which states that “in the absence of any prior knowledge, we must assume that the events [in 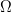 $\Omega$] … have equal probability” [34].
Problem-specific information includes both target-location information
and search-space structure information. Uniformity is equivalent to an
assumption of maximum (informational) entropy on the search space. The assumption of maximum entropy is useful in optimization and is, for example, foundational in Burg's maximum entropy method [6], [9], [34].
$\Omega$] … have equal probability” [34].
Problem-specific information includes both target-location information
and search-space structure information. Uniformity is equivalent to an
assumption of maximum (informational) entropy on the search space. The assumption of maximum entropy is useful in optimization and is, for example, foundational in Burg's maximum entropy method [6], [9], [34].
The probability of choosing an element from 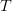 $T$ in
$T$ in 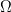 $\Omega$ in a single query is then
$\Omega$ in a single query is then
 TeX Source
$$p = {\vert T\vert\over \vert\Omega\vert}\eqno{\hbox{(1)}}$$ where
TeX Source
$$p = {\vert T\vert\over \vert\Omega\vert}\eqno{\hbox{(1)}}$$ where 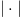 $\vert\cdot\vert$
denotes the cardinality of a set. On the average, without use of active
information, all queries will have this same probability of success.
$\vert\cdot\vert$
denotes the cardinality of a set. On the average, without use of active
information, all queries will have this same probability of success.
For a single query, the available endogenous information is
 TeX Source
$$I_{\Omega} = -\log(p). \eqno{\hbox{(2)}}$$ Endogenous information is independent of the search algorithm used to find the target [39], [46].
To increase the probability of a search success, knowledge concerning
the target location or search-space structure must be prescribed. Let
TeX Source
$$I_{\Omega} = -\log(p). \eqno{\hbox{(2)}}$$ Endogenous information is independent of the search algorithm used to find the target [39], [46].
To increase the probability of a search success, knowledge concerning
the target location or search-space structure must be prescribed. Let 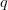 $q$
denote the probability of success of a query by incorporating into the
search problem-specific information. The difficulty of the problem has
changed and is characterized by the exogenous information
$q$
denote the probability of success of a query by incorporating into the
search problem-specific information. The difficulty of the problem has
changed and is characterized by the exogenous information
 TeX Source
$$I_{S} = -\log(q).\eqno{\hbox{(3)}}$$
TeX Source
$$I_{S} = -\log(q).\eqno{\hbox{(3)}}$$
If the problem-specific information incorporated into a search
accurately reflects the target location, the probability of success of a
query will increase. Thus, 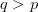 $q > p$ and the corresponding exogenous information will be smaller than the endogenous information (i.e.,
$q > p$ and the corresponding exogenous information will be smaller than the endogenous information (i.e., 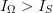 $I_{\Omega} > I_{S}$). The difference between these two information measures we call the active information. It is conveniently represented as
$I_{\Omega} > I_{S}$). The difference between these two information measures we call the active information. It is conveniently represented as
 TeX Source
$$I_{+} = -\log\left({p \over q}\right).\eqno{\hbox{(4)}}$$
This definition satisfies important boundary criteria that are
consistent with properties we expect of problem-specific information.
TeX Source
$$I_{+} = -\log\left({p \over q}\right).\eqno{\hbox{(4)}}$$
This definition satisfies important boundary criteria that are
consistent with properties we expect of problem-specific information.
- For a perfect search,
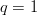 $q = 1$, and the active information is
$q = 1$, and the active information is 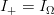 $I_{+} = I_{\Omega}$. The perfect search therefore extracts all available information from the search space.
$I_{+} = I_{\Omega}$. The perfect search therefore extracts all available information from the search space.
- If there is no improvement, the probability of success is the same as that of a random query and
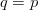 $q = p$. The active information in (4)
is appropriately zero, and no knowledge of the target location or
search-space structure has been successfully incorporated into the
search.
$q = p$. The active information in (4)
is appropriately zero, and no knowledge of the target location or
search-space structure has been successfully incorporated into the
search.
- If the active information degrades performance, then we can have
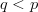 $q < p$ in which case the active information is negative.
$q < p$ in which case the active information is negative.
As with other log-ratio measures, such as decibels, the active
information measure is taken with respect to a reference or baseline, in
this case the chance of success of a single random query 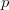 $p$. Other baselines can be used.
$p$. Other baselines can be used.
Single queries generalize directly to multiple queries or samples.
Obtaining one or more sixes in four or less rolls of a die, for example,
can be considered a target 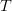 $T$
in a fourfold Cartesian product of the sample space of a single die.
Thus, the sequence of four queries can be considered as a single query
in this larger search space. References to a single query can therefore
correspond to a number of experiments rather than a single measurement.
$T$
in a fourfold Cartesian product of the sample space of a single die.
Thus, the sequence of four queries can be considered as a single query
in this larger search space. References to a single query can therefore
correspond to a number of experiments rather than a single measurement.
Active information captures numerically the problem-specific
information that assists a search in reaching a target. We therefore
find it convenient to use the term “active information” in two
equivalent ways:
- as the specific information about target location and
search-space structure incorporated into a search algorithm that guides a
search to a solution;
- as the numerical measure for this information and defined as the difference between endogenous and exogenous information.
Search often requires numerous queries to achieve success. If 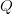 $Q$ queries are required to extract all of the available endogenous information, then the average active information per query is
$Q$ queries are required to extract all of the available endogenous information, then the average active information per query is
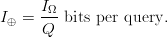 TeX Source
$$I_{\oplus} = {I_{\Omega}\over Q}\ \hbox{bits per query}.$$
TeX Source
$$I_{\oplus} = {I_{\Omega}\over Q}\ \hbox{bits per query}.$$
SECTION III
EXAMPLES OF ACTIVE INFORMATION IN SEARCH
We next illustrate how active information can be measured and offer,
as examples, the active information for search using the common tools of
evolutionary search in commonly used search algorithms, including
repeated queries, importance sampling, partitioned search, evolution
strategy, and use of random mutation. In each case, the source of active
information is identified and is then measured.
D. FOO
Frequency-of-occurrence (FOO) search is applicable for searching for a sequence of 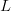 $L$ sequential elements using an alphabet of
$L$ sequential elements using an alphabet of 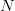 $N$ characters. With no active information, a character must be assumed to occur at the same rate as any other character. Active information can be bettered by querying in accordance to the FOO of the characters [5], [41]. The endogenous information using a uniform distribution is
$N$ characters. With no active information, a character must be assumed to occur at the same rate as any other character. Active information can be bettered by querying in accordance to the FOO of the characters [5], [41]. The endogenous information using a uniform distribution is
 TeX Source
$$I_{\Omega} = L\log_{2}N.\eqno{\hbox{(9)}}$$A priori
knowledge that certain characters occur more frequently than others can
improve the search probability. In such cases, the average information
per character reduces from
TeX Source
$$I_{\Omega} = L\log_{2}N.\eqno{\hbox{(9)}}$$A priori
knowledge that certain characters occur more frequently than others can
improve the search probability. In such cases, the average information
per character reduces from 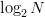 $\log_{2}N$ to the average information or entropy
$\log_{2}N$ to the average information or entropy
 TeX Source
$$H_{N} = -\sum_{n = 1}^{N}p_{n}\log(p_{n})\eqno{\hbox{(10)}}$$ where
TeX Source
$$H_{N} = -\sum_{n = 1}^{N}p_{n}\log(p_{n})\eqno{\hbox{(10)}}$$ where 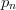 $p_{n}$ is the probability of choosing the
$p_{n}$ is the probability of choosing the 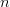 $n$th character.The active information per character is then 1
$n$th character.The active information per character is then 1
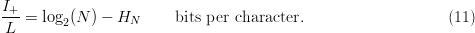 TeX Source
$${I_{+}\over L} = \log_{2}(N) - H_{N}\qquad \hbox{bits per character}.\eqno{\hbox{(11)}}$$
TeX Source
$${I_{+}\over L} = \log_{2}(N) - H_{N}\qquad \hbox{bits per character}.\eqno{\hbox{(11)}}$$
If capitalization and punctuation are not used, English has an alphabet of size 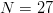 $N = 27$ (26 letters and a space).Some letters, like
$N = 27$ (26 letters and a space).Some letters, like 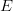 $E$, occur more frequently than others, like
$E$, occur more frequently than others, like 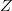 $Z$. Use of FOO information reduces the entropy from
$Z$. Use of FOO information reduces the entropy from 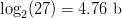 $\log_{2}(27) = 4.76\ \hbox{b}$ to an entropy of about
$\log_{2}(27) = 4.76\ \hbox{b}$ to an entropy of about 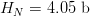 $H_{N} = 4.05\ \hbox{b}$ per character [5]. The active information per character is
$H_{N} = 4.05\ \hbox{b}$ per character [5]. The active information per character is
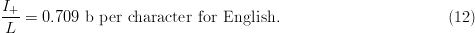 TeX Source
$${I_{+}\over L} = 0.709\ \hbox{b per character for English}.\eqno{\hbox{(12)}}$$
TeX Source
$${I_{+}\over L} = 0.709\ \hbox{b per character for English}.\eqno{\hbox{(12)}}$$
DNA has an alphabet of length 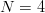 $N = 4$
corresponding to the four nucleotide A, C, G, and T. When equiprobable,
each nucleotide therefore corresponds to 2 b of information per
nucleotide. The human genome has been compressed to a rate of 1.66 b per nucleotide [27] and corresponds to an active information per nucleotide of
$N = 4$
corresponding to the four nucleotide A, C, G, and T. When equiprobable,
each nucleotide therefore corresponds to 2 b of information per
nucleotide. The human genome has been compressed to a rate of 1.66 b per nucleotide [27] and corresponds to an active information per nucleotide of
 TeX Source
$${I_{+}\over L} = 0.34\ \hbox{b per nucleotide}.\eqno{\hbox{(13)}}$$
TeX Source
$${I_{+}\over L} = 0.34\ \hbox{b per nucleotide}.\eqno{\hbox{(13)}}$$
Active FOO information can shrink the search space significantly. For 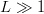 $L\gg 1$, the asymptotic equipartition property [9], [41] becomes applicable. In English, for example, if the probability of choosing an
$L\gg 1$, the asymptotic equipartition property [9], [41] becomes applicable. In English, for example, if the probability of choosing an 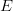 $E$ is 10%, then, as
$E$ is 10%, then, as 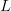 $L$ increases, the proportion of
$L$ increases, the proportion of 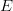 $E$'s in the message will, due to the law of large numbers [33], approach 10% of the elements in the message. Let
$E$'s in the message will, due to the law of large numbers [33], approach 10% of the elements in the message. Let 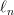 $\ell_{n}$ be the number of elements in a typical message of length
$\ell_{n}$ be the number of elements in a typical message of length 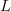 $L$. Then, for large
$L$. Then, for large 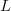 $L$, we can approximate
$L$, we can approximate 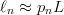 $\ell_{n}\approx p_{n}L$ and
$\ell_{n}\approx p_{n}L$ and
 TeX Source
$$L = \sum_{n = 1}^{N}\ell_{n}.\eqno{\hbox{(14)}}$$
TeX Source
$$L = \sum_{n = 1}^{N}\ell_{n}.\eqno{\hbox{(14)}}$$
Signals wherein (14) is approximately true are called typical. The approximation becomes better as 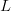 $L$ increases. For a fixed
$L$ increases. For a fixed 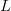 $L$, the number of typical signals can be significantly smaller than
$L$, the number of typical signals can be significantly smaller than 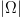 $\vert\Omega \vert$, thereby decreasing the portion of the search space requiring examination.
$\vert\Omega \vert$, thereby decreasing the portion of the search space requiring examination.
To see this, let 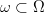 $\omega \subset \Omega$
denote the set of typical signals corresponding to given FOO
probabilities.The added FOO information reduces the size of the search
space from
$\omega \subset \Omega$
denote the set of typical signals corresponding to given FOO
probabilities.The added FOO information reduces the size of the search
space from 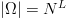 $\vert\Omega\vert = N^{L}$ to 2
$\vert\Omega\vert = N^{L}$ to 2
 TeX Source
$$\vert\omega\vert = 2^{LH_{N}}\eqno{\hbox{(15)}}$$ where
TeX Source
$$\vert\omega\vert = 2^{LH_{N}}\eqno{\hbox{(15)}}$$ where 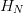 $H_{N}$
is measured in bits. When search is performed using the FOO, the
fractional reduction of size of the search space is specified by the
active information. Specifically
$H_{N}$
is measured in bits. When search is performed using the FOO, the
fractional reduction of size of the search space is specified by the
active information. Specifically
 TeX Source
$${\vert\omega\vert \over\vert\Omega\vert} = {2^{LH_{N}}\over N^{L}} = 2^{-I_{+}}\eqno{\hbox{(16)}}$$ where
TeX Source
$${\vert\omega\vert \over\vert\Omega\vert} = {2^{LH_{N}}\over N^{L}} = 2^{-I_{+}}\eqno{\hbox{(16)}}$$ where 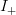 $I_{+}$ is measured in bits. Equation (16) is consistent with (7). For English, from (12), the reduction due to FOO information is
$I_{+}$ is measured in bits. Equation (16) is consistent with (7). For English, from (12), the reduction due to FOO information is 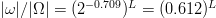 $\vert\omega\vert/\vert\Omega\vert = (2^{-0.709})^{L} = (0.612)^{L}$, a factor quickly approaching zero. From (13), the same is true for the nucleotide sequence for which the effective search-space size reduces by a proportion of
$\vert\omega\vert/\vert\Omega\vert = (2^{-0.709})^{L} = (0.612)^{L}$, a factor quickly approaching zero. From (13), the same is true for the nucleotide sequence for which the effective search-space size reduces by a proportion of 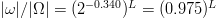 $\vert\omega \vert/\vert\Omega \vert = (2^{-0.340})^{L} = (0.975)^{L}$.
In both cases, the effective reduced search space, though, will still
be too large to practically search even for moderately large values of
$\vert\omega \vert/\vert\Omega \vert = (2^{-0.340})^{L} = (0.975)^{L}$.
In both cases, the effective reduced search space, though, will still
be too large to practically search even for moderately large values of 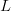 $L$.
$L$.
Yockey [50] offers another bioinformatic application. The amino acids used in protein construction by DNA number 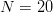 $N = 20$. For a peptide sequence of length
$N = 20$. For a peptide sequence of length 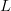 $L$, there are a total of
$L$, there are a total of 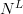 $N^{L}$ possible proteins. For 1-iso-cytochrome c, there are
$N^{L}$ possible proteins. For 1-iso-cytochrome c, there are 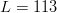 $L = 113$ peptides and
$L = 113$ peptides and 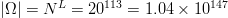 $\vert\Omega\vert = N^{L} = 20^{113} = 1.04\times 10^{147}$
possible combinations. Yockey shows, however, that active FOO
information reduces the number of sequences over 36 orders of magnitude
to
$\vert\Omega\vert = N^{L} = 20^{113} = 1.04\times 10^{147}$
possible combinations. Yockey shows, however, that active FOO
information reduces the number of sequences over 36 orders of magnitude
to 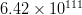 $6.42\times 10^{111}$ possibilities. The search for a specific sequence using this FOO structure supplies about a quarter
$6.42\times 10^{111}$ possibilities. The search for a specific sequence using this FOO structure supplies about a quarter 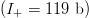 $(I_{+} = 119\ \hbox{b})$ of the required
$(I_{+} = 119\ \hbox{b})$ of the required 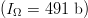 $(I_{\Omega} = 491\ \hbox{b})$ information. The effective search-space size is reduced by a factor of
$(I_{\Omega} = 491\ \hbox{b})$ information. The effective search-space size is reduced by a factor of 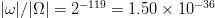 $\vert\omega\vert/\vert\Omega\vert = 2^{-119} = 1.50 \times 10^{-36}$. The reduced size space is still enormous.
$\vert\omega\vert/\vert\Omega\vert = 2^{-119} = 1.50 \times 10^{-36}$. The reduced size space is still enormous.
Active information must be accurate. The asymptotic equipartition
property will work only if the target sought obeys the assigned FOO. As 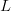 $L$ increases, the match between the target and FOO table must become closer and closer. The boundaries of
$L$ increases, the match between the target and FOO table must become closer and closer. The boundaries of  $\omega$ quickly harden, and any deviation of the target from the FOO will prohibit in finding the target. An extreme example is the curious novel Gadsby [48] which contains no letter
$\omega$ quickly harden, and any deviation of the target from the FOO will prohibit in finding the target. An extreme example is the curious novel Gadsby [48] which contains no letter 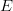 $E$. Imposing a 10% FOO for an
$E$. Imposing a 10% FOO for an 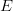 $E$ for even a short passage in Gadsby will nosedive the probability of success to near zero. Negative active information can be fatal to a search.
$E$ for even a short passage in Gadsby will nosedive the probability of success to near zero. Negative active information can be fatal to a search.
E. Partitioned Search
Partitioned search [12] is a “divide and conquer” procedure best introduced by example. Consider the 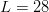 $L = 28$ character phrase
$L = 28$ character phrase
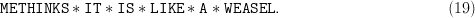 TeX Source
$${\tt METHINKS}\ast{\tt IT}\ast{\tt IS}\ast{\tt LIKE}\ast{\tt A} \ast{\tt WEASEL}.\eqno{\hbox{(19)}}$$ Suppose that the result of our first query of
TeX Source
$${\tt METHINKS}\ast{\tt IT}\ast{\tt IS}\ast{\tt LIKE}\ast{\tt A} \ast{\tt WEASEL}.\eqno{\hbox{(19)}}$$ Suppose that the result of our first query of  $L = 28$ characters is
$L = 28$ characters is
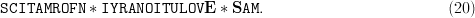 TeX Source
$${\tt SCITAMROFN}\ast{\tt I}{\tt YRANOITULOV}{\bf E}\ast{\bf S}{\tt AM}.\eqno{\hbox{(20)}}$$ Two of the letters
TeX Source
$${\tt SCITAMROFN}\ast{\tt I}{\tt YRANOITULOV}{\bf E}\ast{\bf S}{\tt AM}.\eqno{\hbox{(20)}}$$ Two of the letters 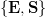 $\{{\bf E}, {\bf S}\}$
are in the correct position. They are shown in a bold font. In
partitioned search, our search for these letters is finished. For the
incorrect letters, we select 26 new letters and obtain
$\{{\bf E}, {\bf S}\}$
are in the correct position. They are shown in a bold font. In
partitioned search, our search for these letters is finished. For the
incorrect letters, we select 26 new letters and obtain
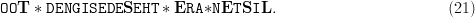 TeX Source
$${\tt OO}{\bf T}\ast{\tt
DENGISEDE}{\bf S}{\tt EHT}\ast{\bf E}{\tt RA}{\bf \ast}{\tt N}{\bf
E}{\tt T}{\bf S}{\tt I}{\bf L}.\eqno{\hbox{(21)}}$$ Five new letters are found, bringing the cumulative tally of discovered characters to
TeX Source
$${\tt OO}{\bf T}\ast{\tt
DENGISEDE}{\bf S}{\tt EHT}\ast{\bf E}{\tt RA}{\bf \ast}{\tt N}{\bf
E}{\tt T}{\bf S}{\tt I}{\bf L}.\eqno{\hbox{(21)}}$$ Five new letters are found, bringing the cumulative tally of discovered characters to 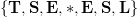 $\{{\bf T}, {\bf S}, {\bf E}, \ast, {\bf E}, {\bf S}, {\bf L}\}$.
All seven characters are ratcheted into place. The 19 new letters are
chosen, and the process is repeated until the entire target phrase is
found.
$\{{\bf T}, {\bf S}, {\bf E}, \ast, {\bf E}, {\bf S}, {\bf L}\}$.
All seven characters are ratcheted into place. The 19 new letters are
chosen, and the process is repeated until the entire target phrase is
found.
Assuming uniformity, the probability of successfully identifying a specified letter with sample replacement at least once in  $Q$ queries is
$Q$ queries is  $1 - (1 - 1/N)^{Q}$, and the probability of identifying all
$1 - (1 - 1/N)^{Q}$, and the probability of identifying all  $L$ characters in
$L$ characters in 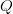 $Q$ queries is
$Q$ queries is
 TeX Source
$$q = \left(1 - \left(1 - \left({1 \over N}\right)\right)^{Q} \right)^{L}.\eqno{\hbox{(22)}}$$
TeX Source
$$q = \left(1 - \left(1 - \left({1 \over N}\right)\right)^{Q} \right)^{L}.\eqno{\hbox{(22)}}$$
For the alternate search using purely random queries of the entire phrase, a sequence of 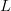 $L$
letters is chosen. The result is either a success and matches the
target phrase, or does not. If there is no match, a completely new
sequence of letters is chosen. To compare partitioned search to purely
random queries, we can rewrite (5) as
$L$
letters is chosen. The result is either a success and matches the
target phrase, or does not. If there is no match, a completely new
sequence of letters is chosen. To compare partitioned search to purely
random queries, we can rewrite (5) as
 TeX Source
$$p = 1 - \left(1 - \left({1 \over N}\right)^{L}\right)^{Q}.\eqno{\hbox{(23)}}$$
TeX Source
$$p = 1 - \left(1 - \left({1 \over N}\right)^{L}\right)^{Q}.\eqno{\hbox{(23)}}$$
For 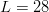 $L = 28$ and
$L = 28$ and 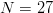 $N = 27$ and moderate values of
$N = 27$ and moderate values of 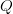 $Q$, we have
$Q$, we have 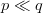 $p \ll q$
corresponding to a large contribution of active information. The active
information is due to knowledge of partial solutions of the target
phrase. Without this knowledge, the entire phrase is tagged as “wrong”
even if it differs from the target by one character.
$p \ll q$
corresponding to a large contribution of active information. The active
information is due to knowledge of partial solutions of the target
phrase. Without this knowledge, the entire phrase is tagged as “wrong”
even if it differs from the target by one character.
The enormous amount of active information provided by partitioned
search is transparently evident when the alphabet is binary. Then,
independent of 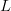 $L$,
convergence can always be performed in two steps. From the first query,
the correct and incorrect bits are identified. The incorrect bits are
then complemented to arrive at the correct solution. Generalizing to an
alphabet of
$L$,
convergence can always be performed in two steps. From the first query,
the correct and incorrect bits are identified. The incorrect bits are
then complemented to arrive at the correct solution. Generalizing to an
alphabet of 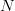 $N$ characters, a phrase of arbitrary length
$N$ characters, a phrase of arbitrary length 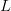 $L$ can always be identified in, at most,
$L$ can always be identified in, at most, 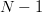 $N - 1$
queries. The first character is offered, and the matching characters in
the phrase are identified and frozen in place. The second character is
offered, and the process is repeated. After repeating the procedure
$N - 1$
queries. The first character is offered, and the matching characters in
the phrase are identified and frozen in place. The second character is
offered, and the process is repeated. After repeating the procedure 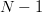 $N - 1$ times, any phrase characters not yet identified must be the last untested element in the alphabet.
$N - 1$ times, any phrase characters not yet identified must be the last untested element in the alphabet.
Partitioned search can be applied at different granularities. We can,
for example, apply partitioned search to entire words rather than
individual letters. Let there be 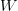 $W$ words each with
$W$ words each with 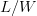 $L/W$ characters each. Then, partitioned search probability of success after
$L/W$ characters each. Then, partitioned search probability of success after 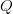 $Q$ queries is
$Q$ queries is
 TeX Source
$$p_{W} = \left(1 - \left(1 - N^{-L/W}\right)^{Q}\right)^{W}.\eqno{\hbox{(24)}}$$ Equations (22) and (23) are special cases for
TeX Source
$$p_{W} = \left(1 - \left(1 - N^{-L/W}\right)^{Q}\right)^{W}.\eqno{\hbox{(24)}}$$ Equations (22) and (23) are special cases for 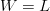 $W = L$ and
$W = L$ and 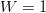 $W = 1$. If
$W = 1$. If 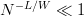 $N^{-L/W} \ll 1$, we can make the approximation
$N^{-L/W} \ll 1$, we can make the approximation 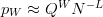 $p_{W}\approx Q^{W}N^{-L}$ from which it follows that the active information is
$p_{W}\approx Q^{W}N^{-L}$ from which it follows that the active information is
 TeX Source
$$I_{+} \approx W\log_{2}Q.\eqno{\hbox{(25)}}$$ With reference to (6), the active information is that of
TeX Source
$$I_{+} \approx W\log_{2}Q.\eqno{\hbox{(25)}}$$ With reference to (6), the active information is that of 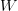 $W$ individual searches: one for each word.
$W$ individual searches: one for each word.
F. Random Mutation
In random mutation, the active information comes from the following sources.
- Choosing the most fit among mutated possibilities. The active information comes from knowledge of the fitness.
- As is the case of prolonged random search, in the sheer number of
offspring. In the extreme, if the number of offspring is equal to the
cardinality of the search space and all different, a successful search
can be guaranteed.
We now offer examples of measuring the active information for these sources of mutation-based search procedures.
1) Choosing the Fittest of a Number of Mutated Offspring
In evolutionary search, a large number of offspring is often
generated, and the more fit offspring are selected for the next
generation. When some offspring are correctly announced as more fit than
others, external knowledge is being applied to the search, giving rise
to active information. As with the child's game of finding a hidden
object, we are being told, with respect to the solution, whether we are
getting “colder” or “warmer” to the target.
Consider the special case where a single parent gives rise to 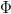 $\Phi$
children. The single child with the best fitness is chosen and used as
the parent for the next generation. If there is even a small chance of
improvement by mutation, the number of children can always be chosen to
place the chance of improvement arbitrarily close to one. To show this,
let
$\Phi$
children. The single child with the best fitness is chosen and used as
the parent for the next generation. If there is even a small chance of
improvement by mutation, the number of children can always be chosen to
place the chance of improvement arbitrarily close to one. To show this,
let 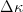 $\Delta\kappa$ be the improvement in fitness. Let the cumulative distribution of
$\Delta\kappa$ be the improvement in fitness. Let the cumulative distribution of 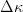 $\Delta\kappa$ be
$\Delta\kappa$ be 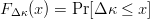 $F_{\Delta \kappa}(x) = \Pr[\Delta\kappa \leq x]$. Requiring there be some chance that a single child will have a better fitness is assured by requiring
$F_{\Delta \kappa}(x) = \Pr[\Delta\kappa \leq x]$. Requiring there be some chance that a single child will have a better fitness is assured by requiring 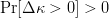 $\Pr[\Delta\kappa > 0] > 0$ or, equivalently,
$\Pr[\Delta\kappa > 0] > 0$ or, equivalently, 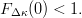 $F_{\Delta\kappa}(0) < 1.$ Generate
$F_{\Delta\kappa}(0) < 1.$ Generate 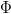 $\Phi$ children, and choose the single fittest. The resulting change of fitness will be
$\Phi$ children, and choose the single fittest. The resulting change of fitness will be 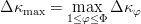 $\Delta\kappa_{\max} = \mathop{\max} \limits_{1\leq \varphi \leq \Phi}\Delta\kappa_{\varphi}$, where
$\Delta\kappa_{\max} = \mathop{\max} \limits_{1\leq \varphi \leq \Phi}\Delta\kappa_{\varphi}$, where 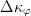 $\Delta\kappa_{\varphi}$ is the change in fitness of child
$\Delta\kappa_{\varphi}$ is the change in fitness of child 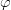 $\varphi$. It follows that
$\varphi$. It follows that 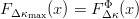 $F_{\Delta\kappa_{\max}}(x) = F_{\Delta \kappa}^{\Phi}(x)$ so that the probability the fitness increases is
$F_{\Delta\kappa_{\max}}(x) = F_{\Delta \kappa}^{\Phi}(x)$ so that the probability the fitness increases is
 TeX Source
$$Pr[\Delta\kappa_{\max} > 0] = 1 - F_{\Delta\kappa}^{\Phi}(0). \eqno{\hbox{(26)}}$$ Since
TeX Source
$$Pr[\Delta\kappa_{\max} > 0] = 1 - F_{\Delta\kappa}^{\Phi}(0). \eqno{\hbox{(26)}}$$ Since 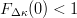 $F_{\Delta\kappa}(0) < 1$, this probability can be placed arbitrarily close to one by choosing a large enough number of children
$F_{\Delta\kappa}(0) < 1$, this probability can be placed arbitrarily close to one by choosing a large enough number of children 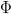 $\Phi$. If we define success of a single generation as better fitness, the active information of having
$\Phi$. If we define success of a single generation as better fitness, the active information of having 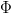 $\Phi$ children as opposed to one is
$\Phi$ children as opposed to one is
 TeX Source
$$I_{+} = -\log\left({1 - F_{\Delta\kappa}^{\Phi}(0)\over 1 - F_{\Delta\kappa}(0)}\right).\eqno{\hbox{(27)}}$$
TeX Source
$$I_{+} = -\log\left({1 - F_{\Delta\kappa}^{\Phi}(0)\over 1 - F_{\Delta\kappa}(0)}\right).\eqno{\hbox{(27)}}$$
2) Optimization by Mutation
Optimization by mutation, a type of stochastic search, discards
mutations with low fitness and propagates those with high fitness. To illustrate, consider a single-parent version of a simple mutation algorithm analyzed by McKay [32]. Assume a binary 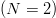 $(N = 2)$ alphabet and a phrase of
$(N = 2)$ alphabet and a phrase of 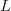 $L$ bits. The first query consists of
$L$ bits. The first query consists of 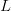 $L$ randomly selected binary digits. We mutate the parent with a bit-flip probability of
$L$ randomly selected binary digits. We mutate the parent with a bit-flip probability of 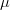 $\mu$
and form two children. The fittest child, as measured by the Hamming
distance from the target, serves as the next parent, and the process is
repeated. Choosing the fittest child is the source of the active
information. When
$\mu$
and form two children. The fittest child, as measured by the Hamming
distance from the target, serves as the next parent, and the process is
repeated. Choosing the fittest child is the source of the active
information. When 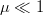 $\mu \ll 1$, the search is a simple Markov birth process [34] that converges to the target.
$\mu \ll 1$, the search is a simple Markov birth process [34] that converges to the target.
To show this, let 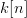 $k[n]$ be the number of correct bits on the
$k[n]$ be the number of correct bits on the 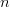 $n$th iteration. For an initialization of
$n$th iteration. For an initialization of 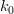 $k_{0}$, we show in the Appendix that the expected value of this iteration is
$k_{0}$, we show in the Appendix that the expected value of this iteration is
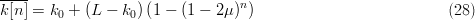 TeX Source
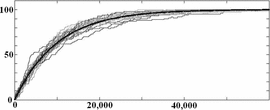
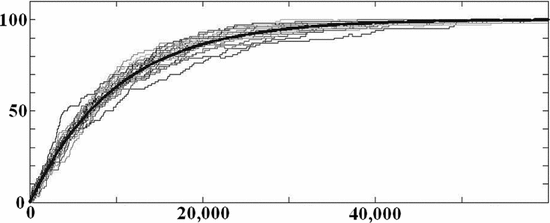
$$\overline{k[n]} = k_{0} + (L - k_{0})\left(1 - (1 - 2\mu)^{n}\right)\eqno{\hbox{(28)}}$$ where the overbar denotes expectation. Example simulations are shown in Fig. 2.
TeX Source
$$\overline{k[n]} = k_{0} + (L - k_{0})\left(1 - (1 - 2\mu)^{n}\right)\eqno{\hbox{(28)}}$$ where the overbar denotes expectation. Example simulations are shown in Fig. 2.
The endogenous information of the search is 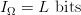 $I_{\Omega} = L\ \hbox{bits}$. Let us estimate that this information is achieved by a perfect search in
$I_{\Omega} = L\ \hbox{bits}$. Let us estimate that this information is achieved by a perfect search in 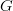 $G$ generations when
$G$ generations when 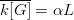 $\overline{k[G]} = \alpha L$ and
$\overline{k[G]} = \alpha L$ and  $\alpha$ is very close to one. Assume
$\alpha$ is very close to one. Assume 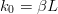 $k_{0} = \beta L$. Then
$k_{0} = \beta L$. Then
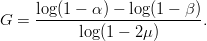 TeX Source
$$G = {\log(1 - \alpha) - \log(1 - \beta)\over\log(1 - 2\mu)}.$$ A reasonable assumption is that half of the initially chosen random bits are correct, and
TeX Source
$$G = {\log(1 - \alpha) - \log(1 - \beta)\over\log(1 - 2\mu)}.$$ A reasonable assumption is that half of the initially chosen random bits are correct, and 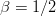 $\beta = 1/2$. Set
$\beta = 1/2$. Set 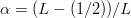 $\alpha = (L - (1/2))/L$. Then, since the number of queries is
$\alpha = (L - (1/2))/L$. Then, since the number of queries is 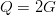 $Q = 2G$, the number of queries for a perfect search
$Q = 2G$, the number of queries for a perfect search 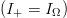 $(I_{+} = I_{\Omega})$ is
$(I_{+} = I_{\Omega})$ is
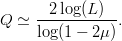 TeX Source
$$Q \simeq {2\log(L) \over \log(1 - 2\mu)}.$$ The average active information per query is thus
TeX Source
$$Q \simeq {2\log(L) \over \log(1 - 2\mu)}.$$ The average active information per query is thus
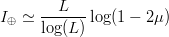 TeX Source
$$I_{\oplus} \simeq {L \over \log(L)}\log(1 - 2\mu)$$ or, since
TeX Source
$$I_{\oplus} \simeq {L \over \log(L)}\log(1 - 2\mu)$$ or, since 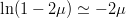 $\ln(1 - 2\mu) \simeq -2 \mu$ for
$\ln(1 - 2\mu) \simeq -2 \mu$ for 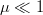 $\mu \ll 1$
$\mu \ll 1$
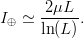 TeX Source
$$I_{\oplus} \simeq {2\mu L \over \ln(L)}.$$ For the example shown in Fig. 2,
TeX Source
$$I_{\oplus} \simeq {2\mu L \over \ln(L)}.$$ For the example shown in Fig. 2, 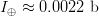 $I_{\oplus} \approx 0.0022\ \hbox{b}$ per query.
$I_{\oplus} \approx 0.0022\ \hbox{b}$ per query.
3) Optimization by Mutation With Elitism
Optimization by mutation with elitism is the same as optimization by mutation in Section III-F2
with the following change. One mutated child is generated. If the child
is better than the parent, it replaces the parent. If not, the child
dies, and the parent tries again. Typically, this process gives birth to
numerous offspring, but we will focus attention on the case of a single
child. We will also assume that there is a single bit flip per
generation.
For 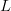 $L$ bits, assume that there are
$L$ bits, assume that there are 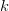 $k$ matches to the target. The chance of improving the fitness is a Bernoulli trial with probability
$k$ matches to the target. The chance of improving the fitness is a Bernoulli trial with probability 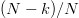 $(N - k)/N$. The number of Bernoulli trials before a success is geometric random variable equal to the reciprocal
$(N - k)/N$. The number of Bernoulli trials before a success is geometric random variable equal to the reciprocal 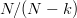 $N/(N - k)$.
We can use this property to map the convergence of optimization by
mutation with elitism. For discussion's sake, assume we start with an
estimate that is opposite of the target at every bit. The initial
Hamming distance between the parent and the target is thus
$N/(N - k)$.
We can use this property to map the convergence of optimization by
mutation with elitism. For discussion's sake, assume we start with an
estimate that is opposite of the target at every bit. The initial
Hamming distance between the parent and the target is thus 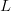 $L$. The chance of an improvement on the first flip is one, and the Hamming distance decreases to
$L$. The chance of an improvement on the first flip is one, and the Hamming distance decreases to 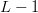 $L - 1$. The chance of the second bit flip to improve the fitness is
$L - 1$. The chance of the second bit flip to improve the fitness is 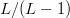 $L/(L - 1)$. We expect
$L/(L - 1)$. We expect 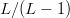 $L/(L - 1)$ flips before the next improvements. The sum of the expected values to achieve a fitness of
$L/(L - 1)$ flips before the next improvements. The sum of the expected values to achieve a fitness of 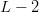 $L - 2$ is therefore
$L - 2$ is therefore
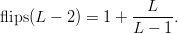 TeX Source
$$\hbox{flips}(L - 2) = 1+ {L \over L - 1}.$$ Likewise
TeX Source
$$\hbox{flips}(L - 2) = 1+ {L \over L - 1}.$$ Likewise
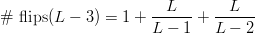 TeX Source
$$\#\ \hbox{flips}(L - 3) = 1+ {L \over L - 1} + {L \over L - 2}$$ or, in general
TeX Source
$$\#\ \hbox{flips}(L - 3) = 1+ {L \over L - 1} + {L \over L - 2}$$ or, in general
 TeX Source
$$\#\ \hbox{flips}(L - \ell) = \sum_{m = 0}^{\ell - 1}{L \over L - m}.\eqno{\hbox{(29)}}$$ It follows that
TeX Source
$$\#\ \hbox{flips}(L - \ell) = \sum_{m = 0}^{\ell - 1}{L \over L - m}.\eqno{\hbox{(29)}}$$ It follows that
 TeX Source
$$\#\ \hbox{flips}(L - \ell) = L[{\cal H}_{L} - {\cal H}_{L - \ell}]\eqno{\hbox{(30)}}$$ where 3
TeX Source
$$\#\ \hbox{flips}(L - \ell) = L[{\cal H}_{L} - {\cal H}_{L - \ell}]\eqno{\hbox{(30)}}$$ where 3
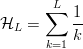 TeX Source
$${\cal H}_{L} = \sum_{k = 1}^{L}{1 \over k}$$ is the
TeX Source
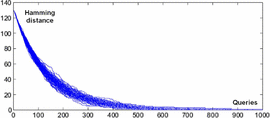
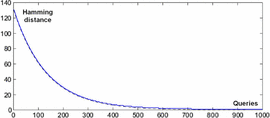
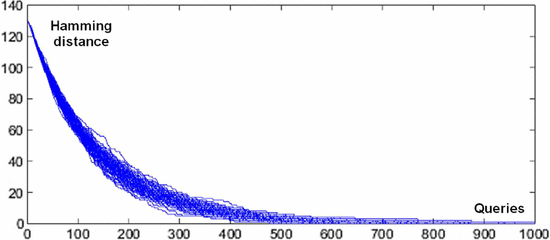
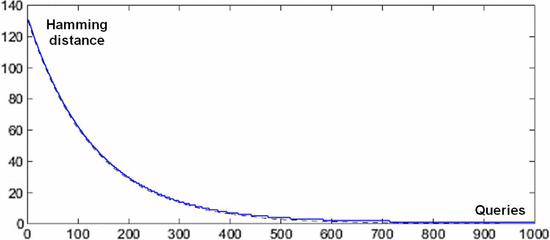
$${\cal H}_{L} = \sum_{k = 1}^{L}{1 \over k}$$ is the 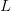 $L$th harmonic number [3]. Simulations are shown in Fig. 3, and a comparison of their average with (30) is in Fig. 4. For
$L$th harmonic number [3]. Simulations are shown in Fig. 3, and a comparison of their average with (30) is in Fig. 4. For 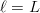 $\ell = L$, we have a perfect search and
$\ell = L$, we have a perfect search and
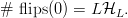 TeX Source
$$\#\ \hbox{flips}(0) = L{\cal H}_{L}.$$ Since the endogenous information is
TeX Source
$$\#\ \hbox{flips}(0) = L{\cal H}_{L}.$$ Since the endogenous information is 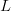 $L$ bits, the active information per query is therefore
$L$ bits, the active information per query is therefore
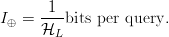 TeX Source
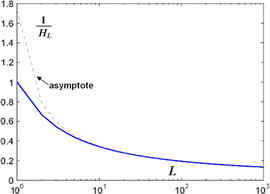
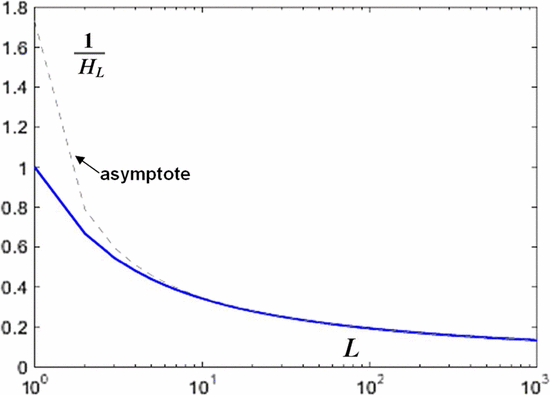
$$I_{\oplus} = {1 \over {\cal H}_{L}}\hbox{bits per query}.$$ This is shown in Fig. 5.
TeX Source
$$I_{\oplus} = {1 \over {\cal H}_{L}}\hbox{bits per query}.$$ This is shown in Fig. 5.
G. Stair-Step Search
By stair-step search, we mean building on more probable search
results to achieve a more difficult search. Like partitioned search,
active information is introduced through knowledge of partial solutions
of the target.
We give an example of stair-step search using FOO. Consider the following sequence of 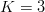 $K = 3$ phrases:
$K = 3$ phrases:
- STONE_;
- TEN_TOES_;
- _TENSE_TEEN_TOOTS_ONE_TONE_TEST_SET_.
The first phrase establishes the characters used. The second
establishes the FOO of the characters. The third has the same character
FOO as the second but is longer. From an 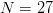 $N = 27$ letter alphabet, the final phrase contains
$N = 27$ letter alphabet, the final phrase contains 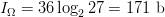 $I_{\Omega} = 36\log_{2}27 = 171\ \hbox{b}$
of endogenous information. To find this phrase, we will first search
for phrase 1 until a success is achieved. Then, using the FOO of phrase
1, search for phrase 2. The FOO of phrase 2 is used to search for phrase
3.
$I_{\Omega} = 36\log_{2}27 = 171\ \hbox{b}$
of endogenous information. To find this phrase, we will first search
for phrase 1 until a success is achieved. Then, using the FOO of phrase
1, search for phrase 2. The FOO of phrase 2 is used to search for phrase
3.
Generally, let 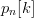 $p_{n}[k]$ be the probability of the
$p_{n}[k]$ be the probability of the 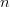 $n$th character in phrase
$n$th character in phrase 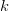 $k$ and let the probability of achieving success for the all of the first
$k$ and let the probability of achieving success for the all of the first 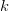 $k$ phrases be
$k$ phrases be 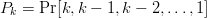 $P_{k} = \Pr[k, k - 1, k - 2, \ldots, 1]$. Then
$P_{k} = \Pr[k, k - 1, k - 2, \ldots, 1]$. Then
 TeX Source
$$P_{k} = P_{k\vert k - 1}P_{k - 1}\eqno{\hbox{(31)}}$$ where the conditional probability is
TeX Source
$$P_{k} = P_{k\vert k - 1}P_{k - 1}\eqno{\hbox{(31)}}$$ where the conditional probability is 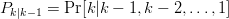 $P_{k\vert k - 1} = \Pr[k\vert k - 1, k - 2, \ldots, 1]$. The process is first-order Markov and can be written as
$P_{k\vert k - 1} = \Pr[k\vert k - 1, k - 2, \ldots, 1]$. The process is first-order Markov and can be written as
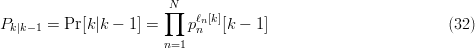 TeX Source
$$P_{k\vert k - 1} = \Pr[k\vert k - 1] = \prod_{n = 1}^{N}p_{n}^{\ell_{n}[k]}[k - 1]\eqno{\hbox{(32)}}$$ where
TeX Source
$$P_{k\vert k - 1} = \Pr[k\vert k - 1] = \prod_{n = 1}^{N}p_{n}^{\ell_{n}[k]}[k - 1]\eqno{\hbox{(32)}}$$ where 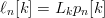 $\ell_{n}[k] = L_{k}p_{n}[k]$ is the occurrence count of the
$\ell_{n}[k] = L_{k}p_{n}[k]$ is the occurrence count of the 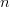 $n$th letter in the
$n$th letter in the 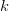 $k$th phrase and
$k$th phrase and 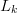 $L_{k}$ is the total number of letters in the
$L_{k}$ is the total number of letters in the 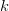 $k$th phrase.Define the information required to find the
$k$th phrase.Define the information required to find the 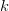 $k$th phrase by
$k$th phrase by 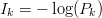 $I_{k} = -\log(P_{k})$. From (31) and (32), it follows that
$I_{k} = -\log(P_{k})$. From (31) and (32), it follows that
 TeX Source
$$I_{k} = I_{k - 1} + L_{k}H(k, k - 1)\eqno{\hbox{(33)}}$$ where the cross entropy between phrase
TeX Source
$$I_{k} = I_{k - 1} + L_{k}H(k, k - 1)\eqno{\hbox{(33)}}$$ where the cross entropy between phrase 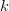 $k$ and
$k$ and 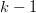 $k - 1$ is [32]
$k - 1$ is [32]
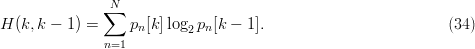 TeX Source
$$H(k, k - 1) = \sum_{n = 1}^{N}p_{n}[k]\log_{2}p_{n}[k - 1].\eqno{\hbox{(34)}}$$
TeX Source
$$H(k, k - 1) = \sum_{n = 1}^{N}p_{n}[k]\log_{2}p_{n}[k - 1].\eqno{\hbox{(34)}}$$
The solution to the difference equation in (33) is
 TeX Source
$$I_{K} = \sum_{k = 1}^{K}L_{k}H(k, k - 1)\eqno{\hbox{(35)}}$$ where
TeX Source
$$I_{K} = \sum_{k = 1}^{K}L_{k}H(k, k - 1)\eqno{\hbox{(35)}}$$ where 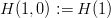 $H(1, 0): = H(1)$. The active information follows as
$H(1, 0): = H(1)$. The active information follows as
 TeX Source
$$I_{+} = I_{\Omega} - I_{K}.\eqno{\hbox{(36)}}$$
TeX Source
$$I_{+} = I_{\Omega} - I_{K}.\eqno{\hbox{(36)}}$$
Use of the 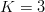 $K = 3$ phrase sequence in our example yields
$K = 3$ phrase sequence in our example yields 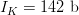 $I_{K} = 142\ \hbox{b}$ corresponding to an overall active information of
$I_{K} = 142\ \hbox{b}$ corresponding to an overall active information of 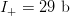 $I_{+} = 29\ \hbox{b}$.
Interestingly, we do better by omitting the second phrase and going
directly from the first to the third phrase. The active information
increases to
$I_{+} = 29\ \hbox{b}$.
Interestingly, we do better by omitting the second phrase and going
directly from the first to the third phrase. The active information
increases to 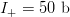 $I_{+} = 50\ \hbox{b}$.4 Each stair step costs information so that a step's contribution to the solution must be weighed against the cost.
$I_{+} = 50\ \hbox{b}$.4 Each stair step costs information so that a step's contribution to the solution must be weighed against the cost.
SECTION IV
CRITIQUING EVOLUTIONARY-SEARCH ALGORITHMS
Christensen and Oppacher [7]
note the “sometimes-outrageous claims that had been made of specific
optimization algorithms.” Their concern is well founded. In computer
simulations of evolutionary search, researchers often construct a
complicated computational software environment and then evolve a group
of agents in that environment. When subjected to rounds of selection and
variation, the agents can demonstrate remarkable success at resolving
the problem in question. Often, the claim is made, or implied, that the
search algorithm deserves full credit for this remarkable success. Such
claims, however, are often made as follows: 1) without numerically or
analytically assessing the endogenous information that gauges the
difficulty of the problem to be solved and 2) without acknowledging,
much less estimating, the active information that is folded into the
simulation for the search to reach a solution.
A. Monkey at a Typewriter
A “monkey at a typewriter” is often used to illustrate the viability
of random evolutionary search. It also illustrates the need for active
information in even modestly sized searches. Consider the production of a
specified phrase by randomly selecting an English alphabet of 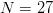 $N = 27$ characters (26 letters and a space). For uniform probability, the chance of randomly generating a message of length
$N = 27$ characters (26 letters and a space). For uniform probability, the chance of randomly generating a message of length 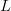 $L$ is
$L$ is 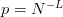 $p = N^{-L}$. The chances are famously small. Presentation of each string of
$p = N^{-L}$. The chances are famously small. Presentation of each string of 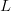 $L$ characters requires
$L$ characters requires 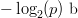 $-\log_{2}(p)\ \hbox{b}$
of information. The expected number of repeated Bernoulli trials (with
replacement) before achieving a success is a geometric random variable
with mean
$-\log_{2}(p)\ \hbox{b}$
of information. The expected number of repeated Bernoulli trials (with
replacement) before achieving a success is a geometric random variable
with mean
 TeX Source
$$Q = {1 \over p}\ \hbox{queries}.\eqno{\hbox{(37)}}$$ Thus, in the search for a specific phrase, we would expect to use
TeX Source
$$Q = {1 \over p}\ \hbox{queries}.\eqno{\hbox{(37)}}$$ Thus, in the search for a specific phrase, we would expect to use
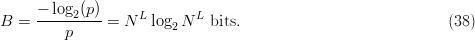 TeX Source
$$B = {-\log_{2}(p) \over p} = N^{L}\log_{2}N^{L}\ \hbox{bits}. \eqno{\hbox{(38)}}$$ Astonishingly, for
TeX Source
$$B = {-\log_{2}(p) \over p} = N^{L}\log_{2}N^{L}\ \hbox{bits}. \eqno{\hbox{(38)}}$$ Astonishingly, for 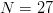 $N = 27$, searching for the
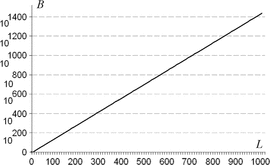
$N = 27$, searching for the 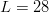 $L = 28$ character message in (19) with no active information requires on average
$L = 28$ character message in (19) with no active information requires on average 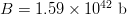 $B = 1.59 \times 10^{42}\ \hbox{b}$—more than the mass of 800 million suns in grams [11]. For
$B = 1.59 \times 10^{42}\ \hbox{b}$—more than the mass of 800 million suns in grams [11]. For 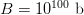 $B = 10^{100}\ \hbox{b}$, more than there are atoms in the universe, solving the transcendental equation in (38) reveals a search capacity for a phrase of a length of only
$B = 10^{100}\ \hbox{b}$, more than there are atoms in the universe, solving the transcendental equation in (38) reveals a search capacity for a phrase of a length of only 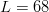 $L = 68$ characters. Even in a multiverse of
$L = 68$ characters. Even in a multiverse of 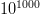 $10^{1000}$ universes the same size as ours, a search can be performed for only
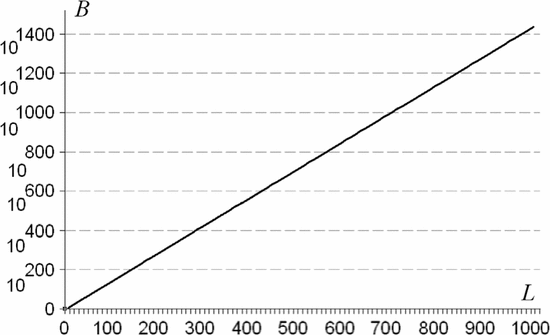
$10^{1000}$ universes the same size as ours, a search can be performed for only 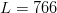 $L = 766$ characters. A plot of the number of bits
$L = 766$ characters. A plot of the number of bits 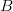 $B$ versus phrase length
$B$ versus phrase length 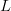 $L$ is shown in Fig. 6 for
$L$ is shown in Fig. 6 for 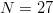 $N = 27$.
$N = 27$.
Active information is clearly required in even modestly sized searches.
Moore's law will not soon overcome these limitations. If we can perform an exhaustive search for a 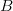 $B$ bit target in 1 h, then, if the computing speed doubles, we will be able to search for
$B$ bit target in 1 h, then, if the computing speed doubles, we will be able to search for 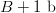 $B + 1\ \hbox{b}$ in the same time period. In the faster mode, we search for
$B + 1\ \hbox{b}$ in the same time period. In the faster mode, we search for 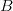 $B$ bits when the new bit is one, and then for
$B$ bits when the new bit is one, and then for 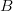 $B$
more bits when the new bit is zero. Each doubling of computer speed
therefore increases our search capabilities in a fixed period of time by
only 1 b. Likewise, for
$B$
more bits when the new bit is zero. Each doubling of computer speed
therefore increases our search capabilities in a fixed period of time by
only 1 b. Likewise, for 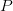 $P$ parallel evaluations, we are able to add only
$P$ parallel evaluations, we are able to add only 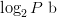 $\log_{2}P\ \hbox{b}$ to the search. Thus, 1024 machines operating in parallel adds only 10 b. Quantum computing can reduce search by a square root [17], [24]. The reduction can be significant but is still not sufficient to allow even moderately sized unassisted searches.
$\log_{2}P\ \hbox{b}$ to the search. Thus, 1024 machines operating in parallel adds only 10 b. Quantum computing can reduce search by a square root [17], [24]. The reduction can be significant but is still not sufficient to allow even moderately sized unassisted searches.
Endogenous information represents the inherent difficulty of a search
problem in relation to a random-search baseline. If any search
algorithm is to perform better than random search, active information
must be resident. If the active information is inaccurate (negative),
the search can perform worse than random. Computers, despite their speed
in performing queries, are thus, in the absence of active information,
inadequate for resolving even moderately sized search problems.
Accordingly, attempts to characterize evolutionary algorithms as
creators of novel information are inappropriate. To have integrity,
search algorithms, particularly computer simulations of evolutionary
search, should explicitly state as follows: 1) a numerical measure of
the difficulty of the problem to be solved, i.e., the endogenous
information, and 2) a numerical measure of the amount of
problem-specific information resident in the search algorithm, i.e., the
active information.
Derivation of (28) in Section III-F2.
Since 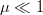 $\mu \ll 1$, terms of order
$\mu \ll 1$, terms of order 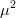 $\mu^{2}$ and higher are discarded. Let
$\mu^{2}$ and higher are discarded. Let 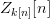 $Z_{k[n]}[n]$ be the number of correct bits that become incorrect on the
$Z_{k[n]}[n]$ be the number of correct bits that become incorrect on the 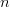 $n$th iteration. We then have the conditional probability
$n$th iteration. We then have the conditional probability
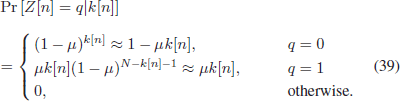 TeX Source
$$\displaylines{\Pr\left[Z[n] =
q\vert k[n]\right]\hfill\cr\hfill = \cases{(1 - \mu)^{k[n]} \approx 1 -
\mu k[n], & $q = 0$\cr\noalign{\vskip3pt} \mu k[n](1 - \mu)^{N -
k[n] - 1} \approx \mu k[n],\qquad & $q = 1$\cr\noalign{\vskip3pt} 0,
& otherwise.}\quad\hbox{(39)}}$$ Similarly, let
TeX Source
$$\displaylines{\Pr\left[Z[n] =
q\vert k[n]\right]\hfill\cr\hfill = \cases{(1 - \mu)^{k[n]} \approx 1 -
\mu k[n], & $q = 0$\cr\noalign{\vskip3pt} \mu k[n](1 - \mu)^{N -
k[n] - 1} \approx \mu k[n],\qquad & $q = 1$\cr\noalign{\vskip3pt} 0,
& otherwise.}\quad\hbox{(39)}}$$ Similarly, let 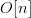 $O[n]$ be the number of incorrect bits that become correct on the
$O[n]$ be the number of incorrect bits that become correct on the 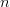 $n$th iteration. Then
$n$th iteration. Then
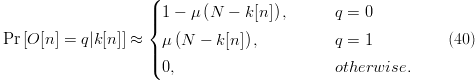 TeX Source
$$\Pr\left[O[n] = q\vert
k[n]\right] \approx \cases{1 - \mu\left(N - k[n]\right),\qquad & $q =
0$\cr\noalign{\vskip3pt} \mu\left(N - k[n]\right), & $q =
1$\cr\noalign{\vskip3pt} 0, & otherwise.}\eqno{\hbox{(40)}}$$ For a given
TeX Source
$$\Pr\left[O[n] = q\vert
k[n]\right] \approx \cases{1 - \mu\left(N - k[n]\right),\qquad & $q =
0$\cr\noalign{\vskip3pt} \mu\left(N - k[n]\right), & $q =
1$\cr\noalign{\vskip3pt} 0, & otherwise.}\eqno{\hbox{(40)}}$$ For a given 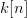 $k[n]$,
$k[n]$, 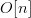 $O[n]$ and
$O[n]$ and 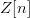 $Z[n]$ are independent Bernoulli random variables. The total chance in fitness is
$Z[n]$ are independent Bernoulli random variables. The total chance in fitness is
 TeX Source
$$\Delta k[n] = Z[n] - O[n].\eqno{\hbox{(41)}}$$
TeX Source
$$\Delta k[n] = Z[n] - O[n].\eqno{\hbox{(41)}}$$
Since 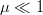 $\mu \ll 1$, the random variable
$\mu \ll 1$, the random variable 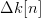 $\Delta k[n]$ can take on values of (−1, 0, 1). The parent is mutated twice, and two mutated children are birthed with fitness changes
$\Delta k[n]$ can take on values of (−1, 0, 1). The parent is mutated twice, and two mutated children are birthed with fitness changes 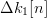 $\Delta k_{1}[n]$ and
$\Delta k_{1}[n]$ and 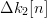 $\Delta k_{2}[n]$. The child with the highest fitness is kept as the parent for the next generation which has a fitness of
$\Delta k_{2}[n]$. The child with the highest fitness is kept as the parent for the next generation which has a fitness of
 TeX Source
$$k[n + 1] = k[n] + \Delta\varkappa[n]\eqno{\hbox{(42)}}$$ where
TeX Source
$$k[n + 1] = k[n] + \Delta\varkappa[n]\eqno{\hbox{(42)}}$$ where 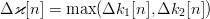 $\Delta \varkappa[n] = \max(\Delta k_{1}[n], \Delta k_{2}[n])$. It then follows that
$\Delta \varkappa[n] = \max(\Delta k_{1}[n], \Delta k_{2}[n])$. It then follows that
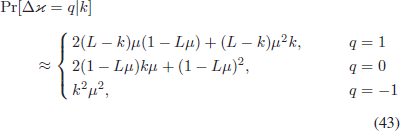 TeX Source
$$\displaylines{\Pr[\Delta\varkappa
= q\vert k]\hfill\cr\hfill \approx \cases{2(L - k)\mu(1 - L\mu) + (L -
k)\mu^{2}k,\qquad & $q = 1$\cr\noalign{\vskip3pt} 2(1 - L\mu)k\mu +
(1 - L\mu)^{2}, & $q = 0$\cr\noalign{\vskip3pt} k^{2}\mu^{2}, &
$q = -1$}\cr\hfill\quad\hbox{(43)}}$$ where we have used a more compact notation, e.g.,
TeX Source
$$\displaylines{\Pr[\Delta\varkappa
= q\vert k]\hfill\cr\hfill \approx \cases{2(L - k)\mu(1 - L\mu) + (L -
k)\mu^{2}k,\qquad & $q = 1$\cr\noalign{\vskip3pt} 2(1 - L\mu)k\mu +
(1 - L\mu)^{2}, & $q = 0$\cr\noalign{\vskip3pt} k^{2}\mu^{2}, &
$q = -1$}\cr\hfill\quad\hbox{(43)}}$$ where we have used a more compact notation, e.g., 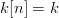 $k[n] = k$. Ridding the equation of
$k[n] = k$. Ridding the equation of 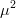 $\mu^{2}$ terms gives
$\mu^{2}$ terms gives
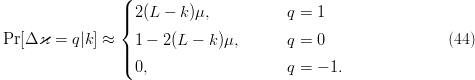 TeX Source
$$\Pr[\Delta\varkappa = q\vert
k] \approx \cases{2(L - k)\mu, & $q = 1$\cr\noalign{\vskip3pt} 1 -
2(L - k)\mu,\qquad & $q = 0$\cr\noalign{\vskip3pt} 0, & $q =
-1.$}\eqno{\hbox{(44)}}$$ Thus, for
TeX Source
$$\Pr[\Delta\varkappa = q\vert
k] \approx \cases{2(L - k)\mu, & $q = 1$\cr\noalign{\vskip3pt} 1 -
2(L - k)\mu,\qquad & $q = 0$\cr\noalign{\vskip3pt} 0, & $q =
-1.$}\eqno{\hbox{(44)}}$$ Thus, for 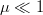 $\mu \ll 1$,
there is a near-zero probability of generating a lower fitness, since
doing so requires both offspring to be of a lower fitness and has a
probability on the order of
$\mu \ll 1$,
there is a near-zero probability of generating a lower fitness, since
doing so requires both offspring to be of a lower fitness and has a
probability on the order of 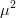 $\mu^{2}$. The mutation search is then recognized as a Markov birth process.
$\mu^{2}$. The mutation search is then recognized as a Markov birth process.
The conditional expected value of (44) is 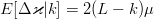 $E[\Delta\varkappa\vert k] = 2(L - k)\mu$. We can then take the expectation of (42) and write
$E[\Delta\varkappa\vert k] = 2(L - k)\mu$. We can then take the expectation of (42) and write 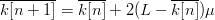 $\overline{k[n + 1]} = \overline{k[n]} + 2(L - \overline{k[n]})\mu$ or, equivalently,
$\overline{k[n + 1]} = \overline{k[n]} + 2(L - \overline{k[n]})\mu$ or, equivalently, 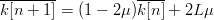 $\overline{k[n + 1]} = (1 - 2\mu)\overline{k[n]} + 2L\mu$, where the overline denotes expectation. The solution of this first-order difference equation is (28).
$\overline{k[n + 1]} = (1 - 2\mu)\overline{k[n]} + 2L\mu$, where the overline denotes expectation. The solution of this first-order difference equation is (28).